This article is a companion to my research paper titled "Graph Coloring Using Heat Diffusion" which can be found here link to research paper. The code to reproduce all results and charts from the research paper can be found here link to code.
A real world case of graph coloring
In this section, I will introduce my readers to a real world situation where we use graph coloring.
Let us assume we are renting out cars (think of your favourite car rental company). We got 6 bookings today. We have to assign a car to each booking.
Booking 1 : 02:00 Hours to 04:00 Hours
Booking 2 : 10:00 Hours to 14:00 Hours
Booking 3 : 02:00 Hours to 08:00 Hours
Booking 4 : 10:00 Hours to 20:00 Hours
Booking 5 : 06:00 Hours to 17:00 Hours
Booking 6 : 18:00 Hours to 24:00 Hours
Plotted against time, the bookings will look like this:
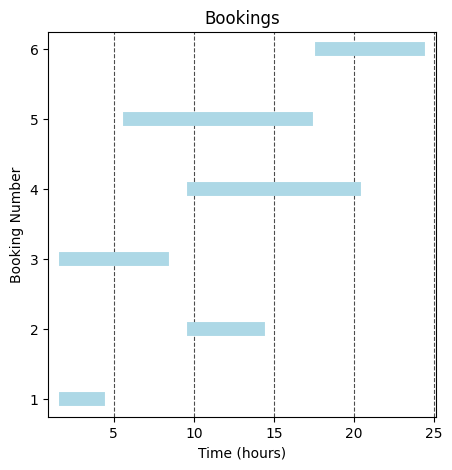
Bookings for the day plotted against time
Here, we want to minimize the number of cars we rent out (to save on maintenance costs). Also, we can't rent out the same car to two bookings that are clashing. For example, booking 1 and book 3 both are clashing from 02:00 Hours to 04:00 Hours.
To better understand these clashes, let us plot an interval graph. The following graph is an interval graph. Each of the nodes represents a booking. The label on each node shows the duration of the booking. If two nodes are connected, that means that they are clashing. For example node (2,4) is connected to node (2,8) because both of them are clashing.
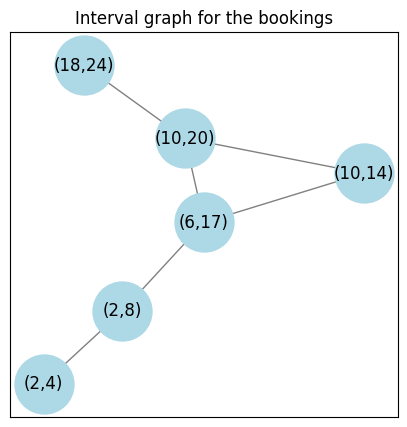
Interval graph for the bookings
Here is the business problem we began with:
We want to assign to assign the minimum number of cars such that no two clashing bookings are assigned the same car
Using the interval graph, we can rephrase the above problem as follows:
We want to assign to assign the minimum number of colors such that no two adjacent nodes are assigned the same color
In the above statement, we framed our business problem as a graph coloring problem. Graph coloring is a computationally challenging problem, and seubsequently, an active area of research. There are a number of algorithms which can solve the graph coloring problem. Some popular ones are the greedy algorithm and Tabu search.
Let us now see what a solution to our problem would look like.
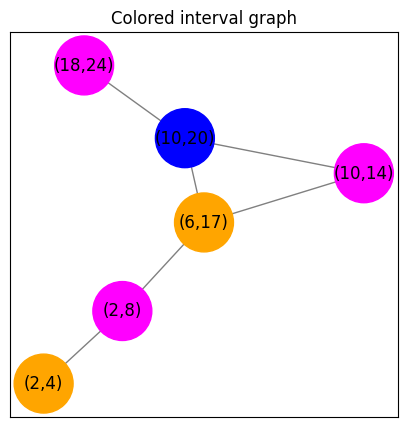
Colored interval graph
In the above graph, we see that no two adjacent nodes are assigned the same color. Also, the nodes are assigned the minimum number of colors possible, which is three. Once we decode this and plot the bookings against time, we get:
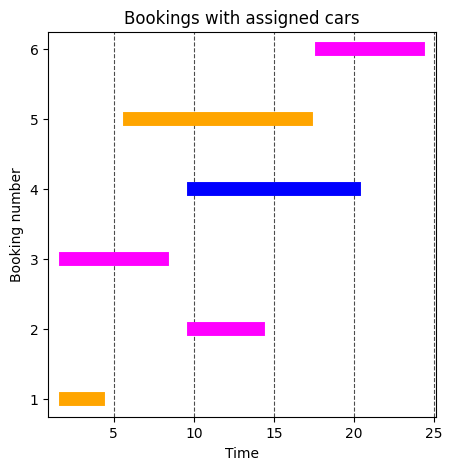
Bookings with assigned cars, each color represents a car
In the above plot we see, booking number 1 and 5 are assigned the same car (orange), since they are not clashing. Boookings 2, 3, and 6 are assigned the same car (magenta) since they do not clash. Booking 4 is assigned the blue car.
